我们都清楚等差数列的求和公式:
以及等比数列的求和公式():
当 且 时几何级数的和
这是一些十分基础且常用的求和公式,本节将详细研究一下这些和式。
我们称上述这些等式右边的不涉及求和号的表达式为 闭型,其不仅简明,而且容易计算。使用归纳法验证上述的公式是十分简单的,但问题在于我们不清楚这些式子是如何得来的。下面简单介绍一些基础的推导方法:
- 扰动法
顾名思义,就是通过观察和式的内在规律,对和式做一些操作使得能轻易求出闭型。具体做什么要根据所求和式决定,16. 母函数 将介绍更多例子。以等比数列求和为例,考虑令
等式两边同乘 有
两式相加得
从而得到上式。
- 逐项求导
将一些常用、已知的和式及其闭型求导可以得到更多和式的闭型。例如我们欲求 的闭型,注意到 ,对上面提到的等比数列求和公式左右求导,容易得到
进一步地,若 ,级数
- 猜测闭型的样子
例如,我们想要求出自然数平方和 的闭型,但这个式子不适合使用扰动法,也无法使用逐项求导。但我们通过对自然数和的闭式进行观察,猜测这个我们要求的式子的闭型可能是一个三次多项式,因此考虑直接令
并通过取 或更多的值,建立关于 的线性方程组,解出系数的值。具体计算过程不表,最终我们会得到
这里的思想在于,如果我们认为求解的式子结果是一个多项式,且推测出了该多项式的最高幂次,就可以通过直接设出该多项式代值得出方程组求解系数。然而,有可能我们的猜想从一开始就是错的,因此当我们得到结果之后,务必要使用归纳法等方法证明结果是对的。
然而并不是所有求和式子都能找到闭型,例如所谓的 调和数(Harmonic Number)
当 时,上式称作 调和级数。
我们通过一个经典问题来直观感受一下调和级数:
将 本长 的书叠放在桌子的边缘,这些书的边缘最多可以伸出桌子边缘多远?假设书是理想刚体,书与书、书与桌子之间不会发生相对滑动。
我们尝试采取递推的方式解决这个问题。设 为堆叠 本书可以伸出的最远距离。先考虑基础情况,一本书时的情况是显然的:将书的重心恰好与桌面边缘对齐,。
接下来,考虑已经成功将 本书堆叠成伸出的距离最远的稳定构型,得到了 ,将这一稳定构型放在另一本直接放在桌面的书上。考虑 本书构成的整体,为了使伸出距离最远,其重心应当恰好与桌面边缘对齐。对于上面的 本书,其重心同样需要在最底部的那本书内,否则就会滑落。同样为了使伸出距离最远,其重心应当恰好与最底部那本书的边缘对齐。因此增加一本书后,多伸出的距离恰好为上面的 本书的重心与桌子边缘(这是原来 本书重心的位置)。这个距离为多少?考虑到最底部的一本书与上面的 本书视作一个整体后整体的重心位于桌面边缘,设想一个如下图所示的杠杆,设伸出距离为 ,依据杠杆平衡很容易得到式子
并解出 ,因此得到递推式 ,展开得到 本书所能伸出的最远距离为
不过尽管没有办法给出该和式的闭型,我们仍然能够构造一些式子来估计它的上下界。
我们首先称一个函数 是 单调递增(或称严格递增)的,当且仅当对任意 有 ; 是 弱递增(或称 单调不减)的,当且仅当对任意 有 ,同理可以定义单调递减函数与弱递减函数。
对于单调函数,我们可以通过对函数积分来粗略估计和式中这一系列离散和的上下界。具体而言:
设 是函数,,。若 是 弱递增 函数,则
对应地,若 是 弱递减 函数,则
此处仅给两张图作示意,具体证明略去。
下限的证明:
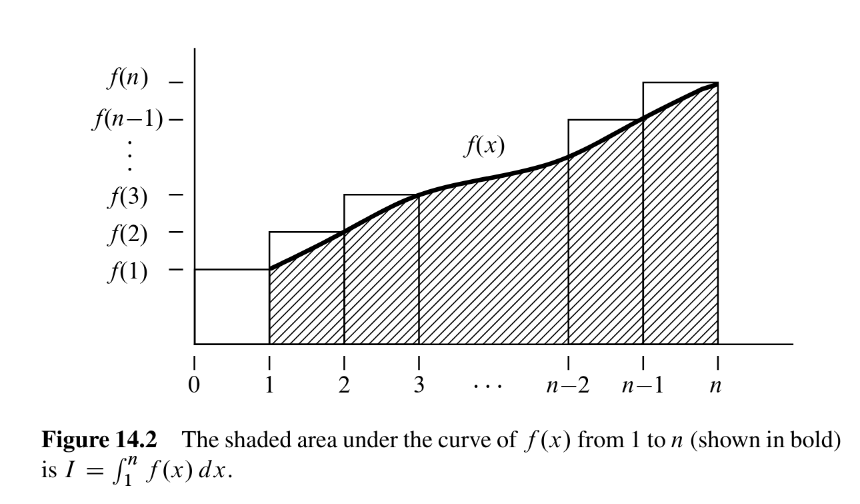
上限的证明:
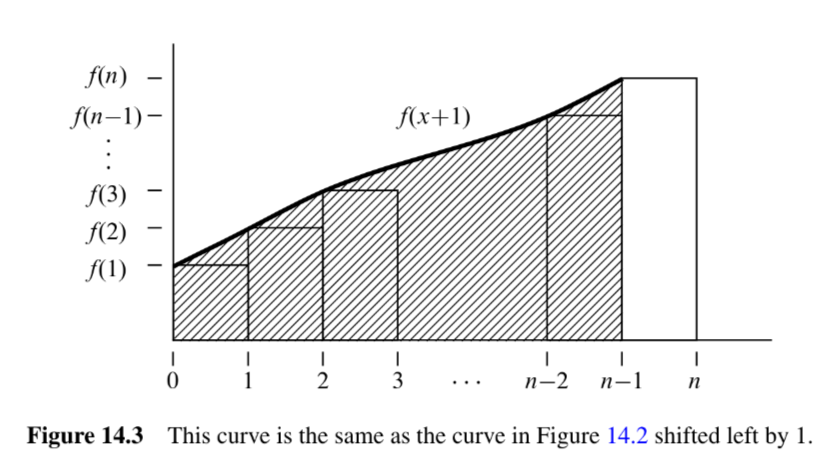
不过由于调和级数非常常见,数学家给出了更加精确的近似:
式中 称作 欧拉常数,约为 , 为余项函数,对任意 满足 ,且随 增大逐渐趋近于 。
有时我们需要计算多重求和号包裹的式子,一般而言,我们希望先算出内层式子的闭型,再一层一层逐步算出整个式子的闭型。如果内部式子没有明显闭型,我们希望能够调换求和顺序,一般也就能解决一大部分多重求和问题了。调换求和顺序的依据是 Fubini 定理,其内容为:
Fubini 定理:
设函数 是定义在 上的可积函数,其中 ,,则重积分
可以分解为任意积分次序的累次积分,即
对离散的求和而言,若求和式子
满足 非负或求和式绝对收敛,则该求和式可以任意调换求和顺序,即
化简
其中 是第 个调和数。
大概了解了和式的处理方法后,我们进一步考虑连乘式,连乘的处理相当简单,对其取对数就能将连乘化为加和。形式化的说,设 ,两边取对得到 ,求出和式的闭型或近似后再取指即可。
我们以 为例,阶乘在组合数学中十分常见。对其取对数后得到的 同样没有闭式。套用上面的过程得到的粗略上下限此处不表。我们直接给出目前 的一个十分精确且重要的估计:
斯特林公式:对任意
式中
上面给出的对调和数与阶乘的近似式子表达形式有点繁琐。我们清楚对调和数而言,式中对最终结果影响最大的项为 ,其余项对结果的影响微乎其微。同理,斯特林公式中的 一般很小,对式子的影响同样可以忽略。因此,我们考虑用一种简洁的方式来表述这一事实:
我们称函数 与函数 渐进相等,当且仅当
记作 。
这样我们可以记 ,更精确一点,我们可以记为 ,但后者不能记作 ,因为依据上面的定义,,其中 为任意常数。类似地,我们记 。
渐进相等主要关注两个函数中对函数增长影响最大的项。当两个函数渐进相等,表明两个函数以相同的速率增长。渐进相等关系与相等关系都是 等价关系。
我们接下来介绍一些其它的渐进符号,这些渐进符号在分析不同算法的理论运行速度上是很有用的。
我们称函数 渐进小于函数 ,当且仅当
记作 。
渐进小于关系是一个严格偏序关系,其表明对于满足 的函数 增长速度是 严格小于 函数 的,通常用于比较两个函数或算法时使用。
小 具有如下性质:
- 若 ,则 。
- 对任意 ,,即对数的增长一定比幂函数缓慢。
- 对任意 ,,即多项式的增长一定比指数函数慢。
与较为严格的渐进小于相对,渐进增长阶 描述了一个函数的 增长上界,为了方便理解,我们记
若
式中 意指 上极限。此时我们记 。
大 符号是分析算法运行效率时最常用的符号。使用大 符号意味着,我们不关心 与 中的低阶项、常数因子,也不关心 是否在某个时刻事实上大于 ,我们只关心 的变化趋势的上界是否在 的常数倍之下,如下图所示:
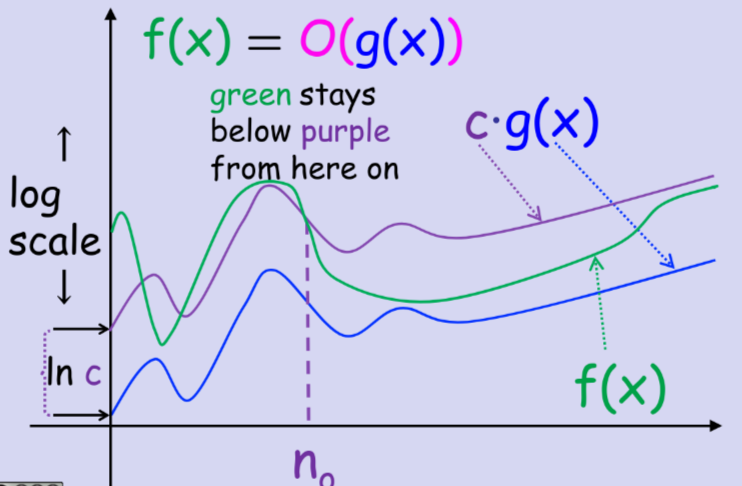
这也是为什么我们在上面的定义中引入了上极限,因为 的极限在无穷大处可能不存在,但我们仍然可以使用大 符号来描述 的增长趋势。
事实上,大 符号的正式定义是这样的:
对函数 与 ,若存在常数 与 ,使得对任意 ,有
那么 。
若 或 ,则 。对应地,该命题的逆命题是错误的,若 ,那么 。
大 符号有如下两条在分析算法运行的时间复杂度时至关重要的性质:
- 对任意 次多项式 ,。
- 对任意常函数 ,。
与渐进小于与描述增长上界的渐进增长阶类似,我们也有描述渐进大于与增长下界的符号:
我们称函数 渐进大于函数 ,当且仅当 ,记作 。
若 ,记 。
当一个函数的渐进上下界相同时,即
若 且 ,记作 。
显然 也是等价关系,但 不等同于渐进相等 。大 忽略了低阶项与常数项对函数增长的影响,其可以被简单理解为,若 ,则 与 的增长速度恰好处在同一个量级。
渐进符号十分好用,但也很容易因为乱用这些渐进符号犯下错误,尤其是大 符号,例如:
- 中的等号不是相等的意思,这个式子也不是一个等式, 也不是一个有具体含义的量,这个式子也不能拆开。我们在后续的数据结构课程中常常见到“程序运行的时间复杂度为 ”的说法是一种方便的简称,严格的说法应该是“程序的运行时间 满足 ”。
- 前面提过, 不是具有确切含义的一个量,因此也不能相加,因此我们不能认为 ,依据本文最开始我们知道 。
- 指数函数中的底数对于函数的增长率影响是巨大的,因此不能随意更改指数,例如 就是不对的。
- 渐进关系在部分复合函数中无法保留,例如 不意味着 ,但确实有一些复合函数可以保留甚至加强这种渐进关系,例如若 ,则 。
最后需要指出的是,虽然一个算法可能拥有更好的渐进时间复杂度,并不意味着实际运行中该算法运行速度会更快。例如,时间复杂度为 的矩阵乘法算法只有在矩阵特别特别大时才有可能比简单的 复杂度算法运行速度更快;再或者,指数复杂度的算法在极小的数据范围下运行速度也可能不会比某阶数极高的多项式复杂度算法慢多少。


